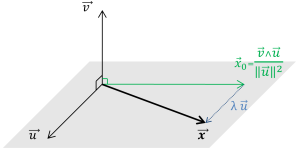
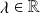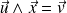Division vectorielle
Soient
L'ensemble des vecteurs
|  |
Complément : Démonstration
On recherche l'ensemble des vecteurs
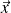tels que
.
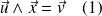Le problème n'a de sens que si les vecteurs
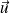et
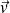sont othogonaux
a) D'une part, on cherche une solution particulière
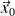de l'équation
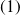appartenant au plan
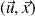telle que :
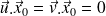
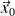est solution de
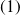si, et seulement si :
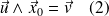
On multiplie vectoriellement à gauche par
:
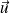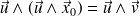
En appliquant la formule de Gibbs il vient :
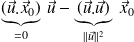d'où :
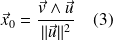
b) D'autre part, par différence entre les équation (1) et (2), il vient :
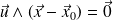
En supposant que
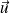et
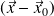soient non nuls, cela signifie que
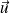et
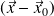sont colinéaires.
Ainsi :
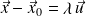avec
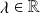
Enfin, en utilisant l'équation
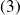, il vient :
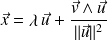avec
