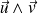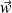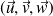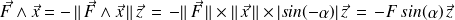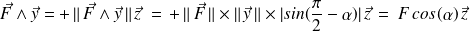C03_Intro : Outils mathématiques pour la mécanique du solide

Afficher le planAfficher le plan

Produit vectoriel

Définition

Définition

Contrairement au produit scalaire, le produit vectoriel a pour résultat un vecteur tel que :

  • direction : est orthogonal au plan formé par et  ;

  • sens : le trièdre est direct ;

  • norme : .

Remarque

Il est également possible de calculer un produit vectoriel à partir des composantes des deux vecteurs à condition que ceux-ci soient exprimés dans une même base :

Soient

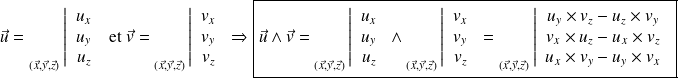
FondamentalMéthode pratique de calcul de produits vectoriels

En pratique, on calculera souvent le résultat d'un produit vectoriel à l'aide de la formule suivante :

\boxed{\, \vec u \wedge \vec v \, = \pm \,\, \Vert \, \vec u \wedge \vec v \, \Vert \,\, \vec n \,}

  • le signe est donné par la règle du tire-bouchon ou des 3 trois doigts de la main droite ;

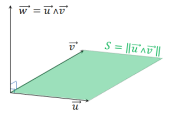
  • le vecteur 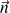correspond au vecteur normal au plan formé par les vecteur 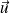et ;

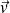  • la norme 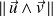se calcule en utilisant la définition du produit vectoriel.

Application :

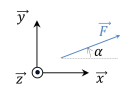FondamentalProduits vectoriels entre vecteurs d'une même base

Soit 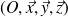un repère orthonormé direct. Le tableau ci-dessous récapitule le résultat des différents produits vectoriels entre deux vecteurs de la même base. Attention toutefois au sens de lecture de ce tableau.

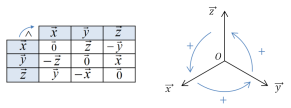
Propriétés

  • Antisymétrie :

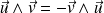
  • Distributivité :

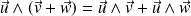
  • Multiplication :

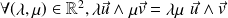
  • Cas de nullité :

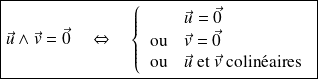
Double produit vectoriel : formule de Gibbs

Pour calculer un double produit vectoriel, on peut utiliser la formule de Gibbs :

\boxed {\vec u \wedge (\vec v \wedge \vec w) = (\vec u . \vec w ) \, \vec v - (\vec u . \vec v) \, \vec w}

En pratique, dans un problème de mécanique, il est souvent plus simple d'effectuer les deux produits vectoriels successifs, en commençant par 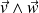. Cette formule reste cependant très utile pour mener à bien certaines démonstrations de théorèmes utilisés en mécanique du solide.

PrécédentPrécédentSuivantSuivant
AccueilAccueilImprimerImprimerRéalisé avec Scenari (nouvelle fenêtre)